Minimax 알고리즘이 뭐에요?
Minimax는 두 플레이어가 번갈아 가며 수를 두는 게임에서 많이 사용되는 알고리즘이다.
- AI는 최대한 좋은 선택을 하려하고 (Maximizer)
- 상대방은 AI에게 최대한 불리한 선택을 하려고 한다 (Minimizer)
- 이 때 가능한 모든 경우의 수를 탐색해서 최적의 수를 결정하는 방식이다.
모든 경우의 수를 내다 보고 가장 높은 점수가 나온 수를 고르는 방식으로
복잡한 게임일수록 계산하는데 오래걸릴 수 있음!
Tic-Tac-Toe로 알아보는 Minimax 알고리즘
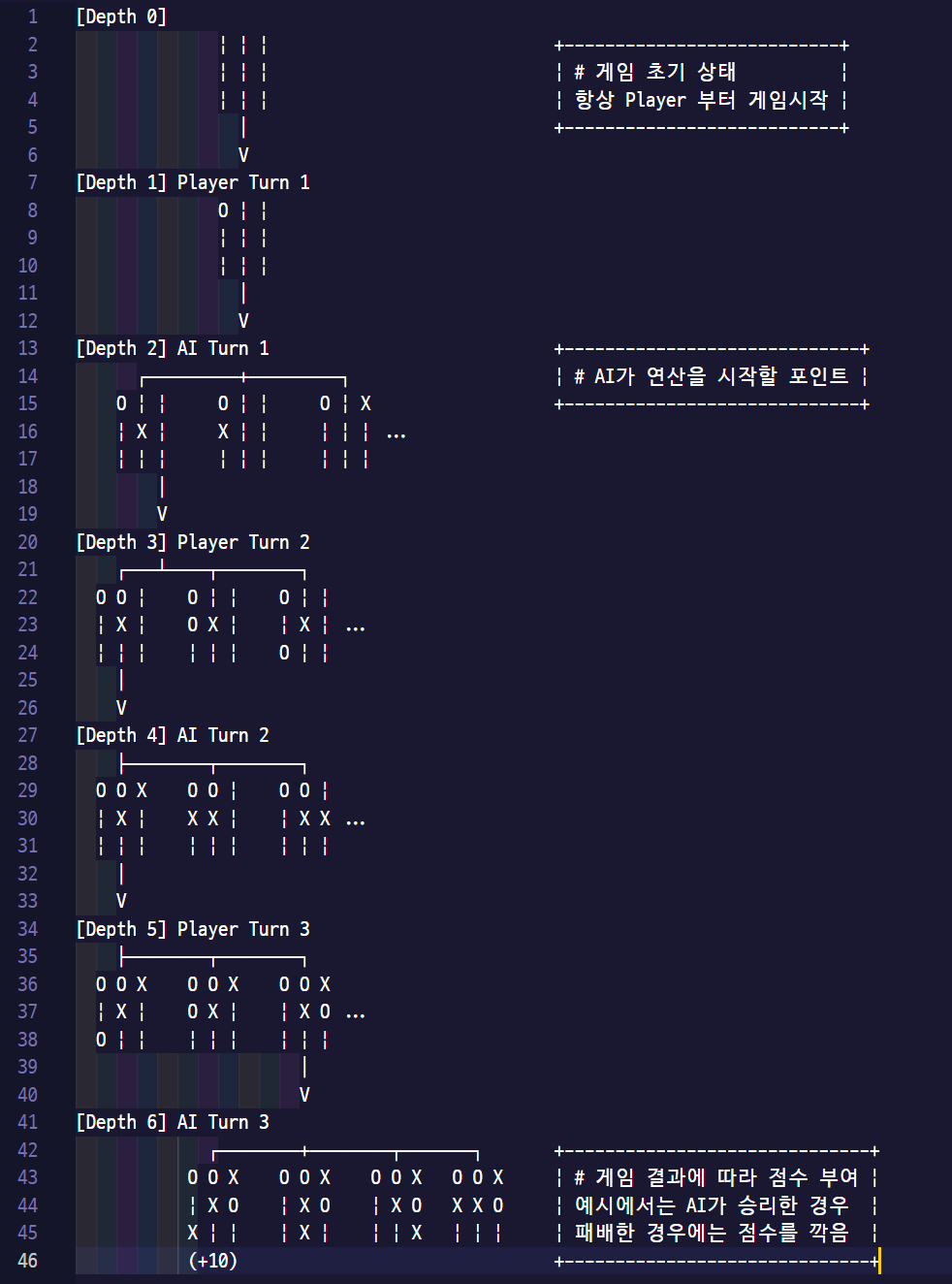
깊이 우선 탐색을 수행하며 끝까지 탐색한 뒤 결과에 따라 점수를 부여한다.
즉, 발생할 수 있는 모든 경우의 수를 탐색한 뒤 결과에 점수를 부여해서 가장 높은 점수를 획득하는 수를 두는 방식이다.
모든 경우의 수를 탐색하기 때문에 바둑, 체스 같은 복잡한 게임에서는 모든 경우의 수를 탐색하는 것은 불가능에 가깝다.
따라서 이를 최적화하기 위해서 Alpha-Beta Pruning같은 최적화 기법을 적용하기도한다.
아래는 기본적인 Unity에서 활용할 수 있는 tic-tac-toe Minimax AI 알고리즘이다.
실제 게임 부분은 제외하고 AI 컨트롤러만 살펴보자.
public class MiniMaxAIController : MonoBehaviour
{
public static (int row, int col)? GetBestMove(GameManager.PlayerType[,] board)
{
int bestScore = int.MinValue;
(int row, int col)? bestMove = null;
for (int row = 0; row < board.GetLength(0); row++)
{
for (int col = 0; col < board.GetLength(1); col++)
{
if (board[row, col] == GameManager.PlayerType.None)
{
board[row, col] = GameManager.PlayerType.PlayerB;
var score = DoMiniMax(board, 0, false);
board[row, col] = GameManager.PlayerType.None;
if (score > bestScore)
{
bestScore = score;
bestMove = (row, col);
}
}
}
}
return bestMove;
}
// Minimax를 수행하기 위한 재귀 함수
private static int DoMiniMax(GameManager.PlayerType[,] board, int depth, bool isAITurn)
{
if (CheckGameWin(GameManager.PlayerType.PlayerA, board))
return -10 + depth; // 빨리 질 수록 더 낮은 점수 부여
if (CheckGameWin(GameManager.PlayerType.PlayerB, board))
return 10 - depth; // 빨리 이기면 더 높은 점수 부여
if (IsAllBlocksPlaced(board))
return 0;
if (isAITurn) // AI턴 가장 유리한 수를 탐색
{
int bestScore = int.MinValue;
for (var row = 0; row < board.GetLength(0); row++)
{
for (var col = 0; col < board.GetLength(1); col++)
{
if (board[row, col] == GameManager.PlayerType.None)
{
board[row, col] = GameManager.PlayerType.PlayerB; // 임시로 마커를 칠함
var score = DoMiniMax(board, depth + 1, false); // 재귀호출
board[row, col] = GameManager.PlayerType.None; // 임시 마커 복구
bestScore = Mathf.Max(bestScore, score);
}
}
}
return bestScore;
}
else // Player의 턴으로 AI에게 최대한 불리한 수를 탐색
{
int bestScore = int.MaxValue;
for (var row = 0; row < board.GetLength(0); row++)
{
for (var col = 0; col < board.GetLength(1); col++)
{
if (board[row, col] == GameManager.PlayerType.None)
{
board[row, col] = GameManager.PlayerType.PlayerA; // 임시로 마커를 칠함
var score = DoMiniMax(board, depth + 1, true); // 재귀 호출
board[row, col] = GameManager.PlayerType.None; // 임시 마커 복구
bestScore = Mathf.Min(bestScore, score);
}
}
}
return bestScore;
}
}
/// <summary>
/// 모든 마커가 보드에 배치 되었는지 확인하는 함수
/// </summary>
/// <returns>True: 모두 배치</returns>
public static bool IsAllBlocksPlaced(GameManager.PlayerType[,] board)
{
for (var row = 0; row < board.GetLength(0); row++)
{
for (var col = 0; col < board.GetLength(1); col++)
{
if (board[row, col] == GameManager.PlayerType.None)
return false;
}
}
return true;
}
/// <summary>
/// 게임의 승패를 판단하는 함수
/// </summary>
/// <param name="playerType"></param>
/// <param name="board"></param>
/// <returns></returns>
private static bool CheckGameWin(GameManager.PlayerType playerType, GameManager.PlayerType[,] board)
{
int length = board.GetLength(0);
// 가로로 마커가 일치하는지 확인
for (var row = 0; row < length; row++)
{
if (board[row, 0] == playerType && board[row, 1] == playerType && board[row, 2] == playerType)
{
return true;
}
}
// 세로로 마커가 일치하는지 확인
for (var col = 0; col < length; col++)
{
if (board[0, col] == playerType && board[1, col] == playerType && board[2, col] == playerType)
{
return true;
}
}
// 대각선 마커 일치하는지 확인
if (board[0, 0] == playerType && board[1, 1] == playerType && board[2, 2] == playerType)
{
return true;
}
if (board[0, 2] == playerType && board[1, 1] == playerType && board[2, 0] == playerType)
{
return true;
}
return false;
}
}
이렇게 작성한 AI는 항상 최적의 수를 찾아내어 수를 반환해주게 된다.
기본적인 Tic-Tac-Toe의 경우 두 플레이어가 최선의 수만 둔다면 반드시 비기게 되어 있기 때문에 절대 이길 수 없는 AI가 탄생한다.
여기에 추가적으로 일정 확율로 실수(빈 칸을 찾아서 아무곳에다 둠)를 하는 로직을 추가하면 적당히 져주는 AI를 만들어 낼 수도 있다.
'Develop > TIL' 카테고리의 다른 글
| [Unity] 싱글톤 GameManager의 상태 갱신 문제 해결 (0) | 2025.02.10 |
|---|---|
| [TIL]Redux-persist 새로고침이 발생해도 store state 유지하기 (0) | 2023.12.03 |
| [TIL] CSS in JS의 성능에 대한 이야기 (0) | 2023.09.09 |
| [TIL] JavaScript의 쓰로틀링과 디바운스 그리고 React (0) | 2023.09.04 |
| [TIL] Hamming Codes: 해밍 코드 (0) | 2023.08.27 |
